DEFINISI
Poligon tertutup adalah poligon yang titik awal dan titik akhirnya bertemu pada satu titik yang sama. Pada poligon tertutup, koreksi sudut dan koreksi koordinat tetap dapat dilakukan walaupun tanpa titik ikat. Poligon tertutup adalah kerangka dasar pengukuran yang membentuk poligon segi banyak yang menutup. Untuk yang dimaksud menutup adalah apabila mulai dari titik 1 kemudian ke titik 2 dan seterusnya akan kembali ke titik 1 lagi, sehingga akan membentuk segi banyak. Fungsi dari kembali ke titik awal adalah digunakan untuk mengkoreksi besaran sudut pada tiap segi banyak tersebut
Pada saat melakukan pengukuran poligon tertutup, kita membidik target muka dan belakang, lalu membaca sudut horizontal dan hasil bacaan tersebut kemudian ditulis pada formulir perhitungan poligon tertutup. Setelah melakukan pengukuran poligon tertutup, langkah selanjutnya adalah kita mengolah data hasil pengukuran poligon tertutup tersebut. Data yang diolah sangat banyak antara lain perhitungan kesalahan penutup sudut, perhitungan sudut yang dikoreksi, perhitungan azimuth, dan sebagainya.
ALUR PERHTUNGAN POLIGON TERTUTUP
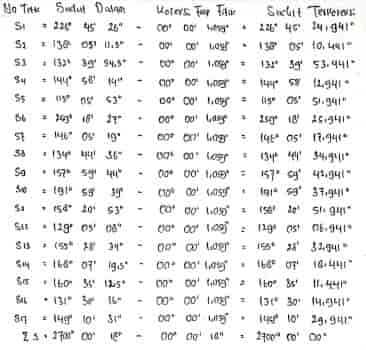
Menentukan Sudut Dalam dan Sudut Luar
Koreksi Sudut/ Kesalahan Penutup Sudut (KPS)
Koreksi Sudut Tiap Titik/ Kesalahan Penutup Sudut Tiap Titik
Sudut Terkoreksi ꞵ i + Koreksi Sudut tiap Titik
Dalam perhitungan sudut terkoreksi tidak melulu ditambah. Contohnya ketika kita mencari koreksi sudut pada poin 2. Ketika ∑α > dari (n-2)x180˚ maka hasilnya akan positif sehinga untuk mencari sudut terkoreksi menjadi dikurang. Jika ∑α < dari (n-2)x180˚ maka akan menghasilkan koreksi sudut negatif, sehingga negatif bertemu tanda kurang akan menjadi positif sehingga ditambah.
Perhitungan Azimut
Cara 1
Cara 2
Perhitungan Absis (∆x) dan Ordinat (∆y)
Perhitungan Koreksi Absis (∆x) dan Ordinat (∆y)
Perhitungan Absis (∆x) dan Ordinat (∆y) Terkoreksi
Pada pengukuran poligon tertutup, hasil penjumlahan dari seluruh titik baik ΔX terkoreksi dan ΔY terkoreksi akan menghasilkan 0,00. Hal ini membuktikan bahwa tidak ada koreksi saat proses perhitungan.
a. X2 = X1 + ΔX 12 Terkoreksi
b. Y2 = Y1 + ΔY 12 Terkoreksi



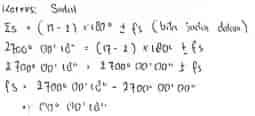














 https://orcid.org/0009-0008-4777-7198
https://orcid.org/0009-0008-4777-7198
.jpg)










Tidak ada komentar:
Posting Komentar